1. Un barco sale de puerto con rumbo N 38º O con velocidad de 25 km/h, un segundo barco parte en el mismo instante con rumbo N 63º E con velocidad de 32 km/h. Determine la distancia que los separa al cabo de 4 horas .
martes, 30 de octubre de 2012
Ley Del Seno Y El Coseno
1. Un barco sale de puerto con rumbo N 38º O con velocidad de 25 km/h, un segundo barco parte en el mismo instante con rumbo N 63º E con velocidad de 32 km/h. Determine la distancia que los separa al cabo de 4 horas .
martes, 28 de agosto de 2012
1 Historia De Grecia
La historia de Grecia es una de las más tempranamente documentadas y estudiadas. Existen fuentes escritas desde el segundo milenio a. C. En la antigüedad Grecia fue una de las regiones con mayor desarrollo tecnológico en Occidente y era poseedora de una rica tradición cultural. Fue famosa por sus conocimientos científicos, sus pensadores y escritores, su arte y sus templos.
2 Bibliografia De Arquimedes
(Siracusa, actual Italia, h. 287 a.C.-id., 212 a.C.) Matemático griego. Hijo de un astrónomo, quien probablemente le introdujo en las matemáticas, Arquímedes estudió en Alejandría
3 Inventos De Arquimedes
El tornillo de Arquímedes
Se quería construir un barco de lujo, para cargas etc… Pero el barco al ser de gran tamaño dejaría pasar grandes cantidades de agua.
La garra de Arquímedes
La garra de Arquímedes era un brazo similar a el de las grúas que Arquímedes usó como arma de asedio contra los barcos romanos.
Los rayos de calor
Usando un sistema combinado con espejos y los rayos de luz solar, con el que consiguió quemar las velas de los barcos romanos
La palanca
Arquímedes inventó la palanca, con la que podía mover grandes objetos con poca fuerza. De ahí su frase celebre “dadme un punto de apoyo y moveré el mundo
La corona dorada:
El rey había pedido como encargo una corona de oro y no estaba muy seguro de que esta fuera exclusivamente de oro, así que pidió a Arquímedes que lo averiguara.
Se quería construir un barco de lujo, para cargas etc… Pero el barco al ser de gran tamaño dejaría pasar grandes cantidades de agua.
La garra de Arquímedes
La garra de Arquímedes era un brazo similar a el de las grúas que Arquímedes usó como arma de asedio contra los barcos romanos.
Los rayos de calor
Usando un sistema combinado con espejos y los rayos de luz solar, con el que consiguió quemar las velas de los barcos romanos
La palanca
Arquímedes inventó la palanca, con la que podía mover grandes objetos con poca fuerza. De ahí su frase celebre “dadme un punto de apoyo y moveré el mundo
La corona dorada:
El rey había pedido como encargo una corona de oro y no estaba muy seguro de que esta fuera exclusivamente de oro, así que pidió a Arquímedes que lo averiguara.
4 Problemas Sobre Torques
Calcular el torque neto por los puntos A y por B en el sistema de
la figura 6.4, donde F
1 = 10 N, F2 = 5 N, F3 = 15 N, a = 50 cm, b = 1 m.Figura.jueves, 7 de junio de 2012
viernes, 13 de abril de 2012
6.4 La Taketina
La taketina es un proceso en grupo, singular y musical. Activa el potencial musical y humano a través del ritmo.
La enseñanza de la taketina abre cada persona la puerta a su talento rítmico.
La enseñanza de la taketina abre cada persona la puerta a su talento rítmico.
6.3 La Matematica Y La Fisica En La Musica
Los teoristas de la música frecuentemente utilizan la matemática para comprender la música.
De hecho matemáticas es la base del sonido y del sonido mismo.
De hecho matemáticas es la base del sonido y del sonido mismo.
6.2 Iniciadores De La Musica
Según la historia, escrita en piedra y no equivoca, la música fue "descubierta" por Pitagoras. Fue el primer hombre que es sus innumerables momentos de devoción cuando no tenia nada que hacer mas que mirar el cielo y quemarse los ojos con el sol, pensó en el viento, en las aves, en que no se cepillo los dientes, en que necesitaba ir al baño y de nuevo pensó en el viento y los sonidos producidos por el, por lo que lo estudio. Descubrió los acordes que se producían en el, por lo que se podría decir que fue el quien descubrió la música.
6.1 Historia De La Musica
Toda la cultura conocida ha tenido alguna forma de manifestación musical, la historia de la música abarca a todas las sociedades y épocas, y no se limita, como ha venido siendo habitual.
sábado, 31 de marzo de 2012
5.1 Historia de la Trígonometría
Historia De La Trigonometria:
Los babilonios y los egipcios fueron los primeros en utilizar los ángulos de un triangulo y las razones trigonometriacas para efectuar medidas en agricultura y para la construcción de pirámides .
.jpg)
Los babilonios y los egipcios fueron los primeros en utilizar los ángulos de un triangulo y las razones trigonometriacas para efectuar medidas en agricultura y para la construcción de pirámides .
5.2 Teorema de Pitágoras
Teorema De Pitagoras:
El teorema de Pitagoras se establece que en un triangulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de lo catetos :
c2 = a2 + b2
El teorema de Pitagoras se establece que en un triangulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de lo catetos :
c2 = a2 + b2
5.3 Relaciones Trígonométricas
Relacione Trigonométricas :
Consideramos que el triangulo rectángulo ABC:
El angulo a cumple que : Sen a = ba y Cos =ca.
Elevamos el cuadrado ambas expresiones: Sen 2 α = b 2 a 2 2 α = c 2 a 2 y las sumamos Sen 2 a + Cos 2 a = b 2 a2 + c2 a2 = b2 + c2 a2 = a2 a2 = 1 . , Sen2 a + Cos2 a = 1 Luego Sen2a + Cos2 a = 1
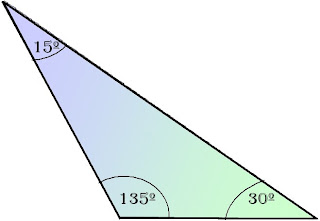
5.4 Teoremas del Seno y del Coseno
Teoremas del Seno:
Los lados de un triangulo son proporcionales a los senos de los ángulos puestos .
a = b = c
Sen A Sen B Sen C
Teorema del Coseno:
a) Cuando conocemos los tres lados.
b) Dos lodos y el angulo opuesto a uno de ellos .
c) Dos lados y el angulo que forma .
b2=a2+c2-2ac cos B=b.
Los lados de un triangulo son proporcionales a los senos de los ángulos puestos .
a = b = c
Sen A Sen B Sen C
a) Cuando conocemos los tres lados.
b) Dos lodos y el angulo opuesto a uno de ellos .
c) Dos lados y el angulo que forma .
b2=a2+c2-2ac cos B=b.
4.2 Triangulo Isósceles
Triangulo Isósceles:
Un triangulo isósceles tiene dos lados y ángulos iguales y uno desigual .
.jpg)
Un triangulo isósceles tiene dos lados y ángulos iguales y uno desigual .
4.3 Triángulo Escaleno
Triangulo Escaleno :
Un triangulo escaleno tiene los tres lados y ángulos desiguales.
4.4 Triángulo Rectángulo
Triángulo Rectángulo:
un triangulo rectángulo tiene un angulo recto y dos agudos.
un triangulo rectángulo tiene un angulo recto y dos agudos.
4.5 Triángulo Acutángulo
Triángulo Acutángulo:
Un triangulo acutángulo tiene los tras ángulos agudos.
.jpg)
Un triangulo acutángulo tiene los tras ángulos agudos.
4.6 Triangulo Obtusángulo
Triangulo Obtusángulo:
El triangulo obtusángulo tiene un angulo obtuso y dos ángulos agudos .
jueves, 29 de marzo de 2012
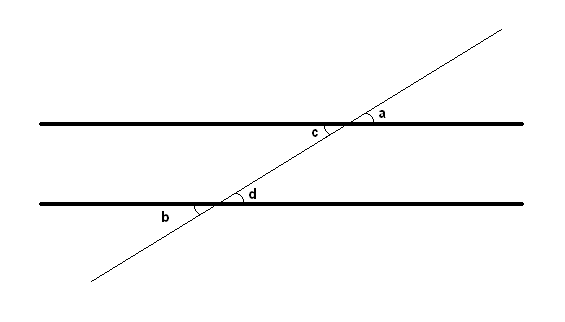
2.4 Recta Paralela y Perpendicular
Rectas Paralelas:
Son dos rectas que se encuentran a cierta distancia y su dirección e inclinación es la misma por lo que nunca se cortan.
Rectas Perpendiculares:
Son dos rectas las cuales están en direcciones contrarias y en un punto determinado se cortan entre si formando cuatro ángulos.
Son dos rectas que se encuentran a cierta distancia y su dirección e inclinación es la misma por lo que nunca se cortan.
Rectas Perpendiculares:
Son dos rectas las cuales están en direcciones contrarias y en un punto determinado se cortan entre si formando cuatro ángulos.
2.3 Mediatriz y Bisectriz
Mediatriz:
la Mediatriz de un segmento es la recta perpendicular al segmento en su punto medio. También se puede definir la Mediatriz de un segmento como el lugar geométrico de los puntos de la plano que equidistan de los extremos del segmento.
Bisectriz:
La Bisectriz de un angulo es la recta que lo divide en dos partes iguales.
la Mediatriz de un segmento es la recta perpendicular al segmento en su punto medio. También se puede definir la Mediatriz de un segmento como el lugar geométrico de los puntos de la plano que equidistan de los extremos del segmento.
Bisectriz:
La Bisectriz de un angulo es la recta que lo divide en dos partes iguales.
2.2 Ángulos y Clases de Ángulos
Definición de Ángulos:
El angulo es una figura que se forma de dos semirrectas las cuales tienen el mismo punto de inicio normalmente se mide esta abertura con grados.
Estas Son Las Clases De Ángulos:
Angulo Recto: es aquel que tiene una abertura de noventa grados.
Angulo Agudo: es el angulo que su abertura es menor de noventa grados.
Angulo Llano: es el angulo que tiene una abertura de ciento ochenta grados.
Angulo Obtuso: es el angulo que su abertura es mayor de noventa grados y menor de ciento ochenta grados.
Angulo Completo: es el angulo que tiene una abertura de trecientos sesenta grados.
El angulo es una figura que se forma de dos semirrectas las cuales tienen el mismo punto de inicio normalmente se mide esta abertura con grados.
Estas Son Las Clases De Ángulos:
Angulo Recto: es aquel que tiene una abertura de noventa grados.
Angulo Agudo: es el angulo que su abertura es menor de noventa grados.
Angulo Llano: es el angulo que tiene una abertura de ciento ochenta grados.
Angulo Obtuso: es el angulo que su abertura es mayor de noventa grados y menor de ciento ochenta grados.
Angulo Completo: es el angulo que tiene una abertura de trecientos sesenta grados.
2.1 Recta , Semirrecta Y Segmento.
Recta Semirrecta Y Segmento.
Recta :
En la recta o lineo recta se extiende en una misma dirección tiene infinitos puntos tiene infinitos segmentos .
Semirrecta :
Una semirrecta es cada una de las partes en que queda dividida una recta por uno o cualquiera de sus puntos.
Segmento
Un segmento es un pedazo de una recta el cual se encuentra entre dos puntos que marca el principio y el fin del segmento.
1.1 Historia De La Geometría Y las Matemáticas
Historia de La Geometría
La geometría es una de las mas antiguas ciencias .Su conocimiento era con las longitudes. Matemáticas Historia
Las Matemáticas es el área de estudio que abarca las investigaciones sobre los orígenes de los descubrimientos en la matemáticas todo sobre los conceptos de este tema y las personas que de una o otra manera están involucrados con dicha historia.
1.2 Filósofos Y Matemáticos
Platon un gran filosofo su pensamiento ejerció una gran influencia en el desarrollo de la filosofía .
.jpg)
.jpg)
Pitagoras
Fue el primer matemático puro tuvo muchas contribuciones atraves de las matemáticas con su teorema .
Veremos Un Video de Pitagoras Y Platon
1.3 ¿Que Es La Geometría?
La geometría es una rama que estudia idealizaciones del espacio: puntos,rectas,planos, polígonos,poliedros,curvas,superficies.
http://www.youtube.com/watch?v=5rXKbuwWh80
3.1 Definición de polígonos
En la geometría un polígono es una figura plana que esta limitada por una curva cerrada , compuestas por una finita de segmentos rectos.
Polígonos Regulares
un polígono regular es aquel que tiene sus ángulos iguales y sus lados iguales
Polígonos Irregulares
Polígonos Regulares
Polígonos Irregulares
los polígonos irregulares no tienen todos sus lados iguales
Suscribirse a:
Entradas (Atom)